[Dieter Grass]

Здравствуйте!

Интересует следующая ситуация:
Вот, люди, меня тут мой руководитель развёл на волновую теорию, а я терь и не знаю, может, то, к чему он меня подтолкнул, и до чего я дошёл, это чушь полная..

Вот смотрите, какие мысли (не пугаться, начну издалека):
1) Функции синус, экспонента и проч - естественные. В том плане, что не человек их придумал, как ему удобно, а что этими простейшими функциями описывается мир вокруг нас: биология, физика, генетика... всё описывается линейной комбинацией этих функций. Вопрос лишь в коэффициентах и сочетаниях

2) В природе имеет место теория колебаний... частный случай - LC-контур, всякие там маятники, шмаятники. Идея в том, что если систему вывести из равновесия, то она будет стремиться в него. Тут можно вспомнить третий закон Ньютона об энтропии (я не помню, но вспомнить можно)

3) Возмущение можно рассматривать как аддитивный (суммирующийся) процесс по отношению к обычному (стационарному) процессу, т.е. при возмущении у нас 2 процесса: нормальный + возмущающий

4) Теоретически после возмущающего воздействия система будет приходить в норму по закону затухающего синуса, т.е. характер будет А sin(kx) * e^(-ax), где x - ключевой параметр системы, описывающий влияние воздействия в том числе, А, k,.a - коэффициенты. Т.е. у нас огибающая - затухающая экспонента, а заполнение - затухающий синус.

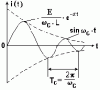
5) Эту теорию можно применить для бизнес-процессов, в частности, для производственного процесса. Но и не только: поступило какое-то возмущающее воздействие, которое резко изменило привычный ритм жизни процесса, а потом система сама или при помощи кого-то вновь возвращается в равновесие (кстати, ведь и не всегда прежний тем восстановится, может, будет другой темп (при сохранении общего характера процесса), а может ведь и сам характер поменяться, и, наконец, система может не справиться и вообще встать наглухо). Но нас интересует те возмущения, после которых потом система восстановится в прежнее рабочее состояние

6) Сами коэффициенты я не знаю как определить, разве что из сравнения с большой практической выборкой, т.е. экспериментальным путём

7) В реале мы имеем не детерминированный, а случайный процесс, который, с некоторым приближением, для рассмотрения можно заменить вышеописанной математической моделью.

8) Теоретически система будет приходить в равновесие бесконечно долго, так как экспонента затухает только на бесконечности, но для практики можно ввести какой-то порог затухания (в процентах от максимума - т.е. во время действия возмущения). Скажем, 5% (то, что в экономике называют несущественным отклонением)

9) С экономической точки зрения, любые отклонения (т.е преодоление коридора, ограничивающего поведение штатного процесса, как верхней границы коридора, так и нижней) означает потери
___________

Вопросы:
1) С чем бы вы поспорили?
2) Можно ли более точно найти формулу для затухания, зная конкретный процесс (скажем, относительный уровень возмущения или ещё что-то)? Конечно, интересует время прихода системы в равновесие (а из него можно вычислить экономические потери от таких возмущений - я так понимаю, ради чего всё это и затевается)
3) Можете ли вы привести какие-то аналоги применения волновой теории в биологии, химии, экономике (что было б совсем замечательно), желательно с ссылками?
Вообще о чём тут речь? сейчас в голову пришла теория ошибок, может, там что-то есть?

Конечно, экономику трудно назвать точной наукой, а российскую - тем более, и даже наукой трудно, но интересует опыт приложения всего этого, куда - уже второй вопрос

Comments

[Rahhal]

В химии хорошей иллюстрацией служит принцип Ле-Шателье: (принцип смещения равновесия), он устанавливает, что внешнее воздействие, выводящее систему из состояния термодинамического равновесия, вызывает в системе процессы, стремящиеся ослабить эффект воздействия. Так, при нагревании равновесной системы в ней происходят изменения (например, химические реакции), идущие с поглощением теплоты, а при охлаждении — изменения, протекающие с выделением теплоты. При увеличении давления смещение равновесия связано с уменьшением общего объёма системы, а уменьшению давления сопутствуют физические или химические процессы, приводящие к увеличению объема.

[Dieter Grass]

Rahhal
т.е. мои рассуждения имеют хотя бы капельку здравого смысла?
сейчас это уже малоактуально, но всё же интересно))